Brainteaser im Bewerbungsgespräch

Was sind Brainteaser?

Brainteaser (englisch: Gehirnkitzler) sind Knobelaufgaben, die in Bewerbungsgesprächen eingesetzt werden. Ein Arbeitgeber versucht mit diesen Rätselaufgaben herauszufinden, wie gut die analytischen Fähigkeiten eines Kandidaten ausgeprägt sind. Brainteaser können dir in Interviews begegnen, aber auch im Assessment-Center oder als Teil eines standardisierten Einstellungstests.

Welche Fähigkeiten brauchst du, um Brainteaser zu lösen?

Um die meisten Brainteaser zu lösen, musst du zugleich logisch, gründlich und kreativ an die Aufgabe herantreten. Oft benötigst du gute mathematische Grundkenntnisse und die Fähigkeit, diese unter Zeitdruck anzuwenden. So solltest du zum Beispiel fähig sein, einen Dreisatz aufzustellen, eine Gleichung aufzulösen, den Umfang eines Kreises zu berechnen oder das Volumen eines Würfels anzugeben. Du wirst auch auf dein visuelles Vorstellungsvermögen angewiesen sein, um dir Aufgaben wie "Benenne den Winkel von Minuten- und Stundenzeiger um 15.15 Uhr" zu vergegenständlichen.

Übe auch, Einheiten ineinander umzurechnen: So kann es wichtig sein, Volumina oder Flächen in kleineren oder größeren Maßstäben auszudrücken. Wie groß war noch mal ein Ar? Und wie viele Kubikmeter passen in einen Kubikkilometer? Auch verschiedene Währungen solltest du ohne langes Zögern "übersetzen" können.

Ebenfalls nicht schaden kann elementares Physikwissen. So sollltest du wissen, wie man bei die Zeit, Geschwindigkeit oder Strecke von konstanten Bewegung berechnen kann: Es gibt nämlich erstaunlich viele Brainteaser, in denen fahrende Züge vorkommen!

Für einige Brainteaser ist es wichtig, möglichst plausible Schätzungen abzugeben. Um nicht zu viel improvisieren zu müssen, solltest du grundlegende demographische Fakten parat haben: So wird man von dir erwarten, die aktuellen Einwohnerzahlen Deutschlands, Europas, der USA und der Welt zu kennen; ferner von Berlin, London und New York. Weitere wichtige Kennzahlen können außerdem Flächen, Bevölkerungsdichten oder Bruttoinlandsprodukte sein; dazu andere grundlegende Daten aus Wirtschaft und Gesellschaft, die in deiner Branche eine Rolle spielen.

Welche Arten von Brainteasern gibt es?

Man kann drei Sorten von Brainteasern unterscheiden:

• "echte" Brainteaser: also mathematische Problemstellungen, Rätsel oder Knobelaufgaben, zu denen sich eine eindeutige Lösung angeben lässt
• Schätzfragen
• Business Cases/Case Studies

Zu den "echten" Brainteasern zählen auch Trickaufgaben oder Fangfragen, deren "richtige" Lösung oft darin besteht, dass es keine richtige Lösung gibt. Die Frage "Wie viel Erde befindet sich in einem Loch mit den Maßen 3 x 2 x 4 m?" ist beispielsweise solch eine Trickfrage – weil sich in einem Loch überhaupt nichts befindet.

Schätzfragen ("Wie schwer ist Manhattan?") dienen dagegen dazu, nachzuweisen, wie schnell und sicher du zu einer bestimmten Annahme gelangst. Neben Faktenwissen benötigst du dazu grundlegende mathematische Kenntnisse und die Fähigkeit, deine empirischen Erfahrungen auf eine größere Skala anzuwenden: So kannst du zum Beispiel versuchen, aus dem Konsumverhalten deines Freundeskreises Aussagen darüber abzuleiten, wie viele Exemplare eines neuen Produkts sich in Deutschland verkaufen lassen.

Um Business Cases zuverlässig zu lösen, musst du oft über methodisches Vorwissen verfügen: Wenn du noch nie von der BCG-Matrix, den 4 Ps, einer SWOT-Analyse oder Porter's Five Forces gehört hast, wirst du bei einer Case Study vermutlich nicht viele Punkte sammeln. Aber keine Sorge: In unserem Buch "Case Study Training" haben wir 40 Fallstudien zusammengestellt, mit denen du dich vorbereiten kannst.

Wer setzt Brainteaser im Bewerbungsgespräch ein?

Brainteaser können dir prinzipiell in jeder Bewerbung begegnen. Besonders beliebt sind sie aber in Bereichen der Finanzbranche, in Unternehmensberatungen und der Kreativbranche. Knobelaufgaben tauchen also immer dort in Interviews auf, wo es darum geht, Probleme genau zu beschreiben, schnell zu analysieren und daraus überraschende Lösungen zu entwickeln.

Sogenannte Business Cases simulieren, wie oben beschrieben, die Arbeit im Consulting und werden dir am ehesten bei McKinsey & Co. begegnen. Um solche Fallstudien angemessen bearbeiten zu können, musst du verschiedene Analyse-Werkzeuge mitbringen, wie sie beispielsweise im BWL-Studium erlernt werden.

Wie löse ich einen Brainteaser im Bewerbungsgespräch richtig?

Da es verschiedene Arten von Brainteasern gibt, existiert auch kein goldener Weg zur jeweiligen Lösung. Grundsätzlich empfehlen wir aber folgendes Vorgehen:

1. Wenn sich eine (zu) offensichtliche Lösung anbietet, ist sie oft falsch.
   Wenn Tischtennisschläger und -ball gemeinsam 1,10 Euro kosten, und der Schläger 1 Euro teurer ist als der Ball – kostet der Ball gerade nicht 10 Cent (sondern 5). Wenn du hier zu schnell mit einer falschen Lösung herausplatzt, beweist du lediglich, dass es dir an Geduld und Reflexionsvermögen mangelt.
   Nimm dir Zeit, bevor du antwortest, und verbalisiere deine Bedenken, wenn du welche hast. Sie sind in der Regel begründet.
2. Lies genau. Oft versteckt sich im Text des Brainteasers schon die gesuchte Lösung, gerade bei Trickfragen.
3. Sind Rückfragen im Interview erlaubt? Wenn ja, nutz die Gelegenheit! Besonders bei Schätzfragen und Cases kannst du so deine Informationsgrundlage bedeutend verbessern – und damit auch dein Ergebnis.
4. Denk laut. Verbalisiere deine Überlegungen, während du über das Problem nachdenkst. Auch mit Gedankenspielen, die nicht direkt zur korrekten Lösung führen, kannst du beweisen, dass du fähig bist, verschiedene kreative Ansätzen anzuwenden, um die Aufgabe zu lösen.
5. Benenn deine Methoden und begründe deine Ergebnisse, selbst wenn die Lösung für dich offensichtlich ist. Wenn du einfach nur das (korrekte) Resultat deine Überlegungen nennst, erweckst du den Eindruck, du hättest die Aufgabe schon gekannt.

20 Brainteaser (mit Tipps & Lösungen)

Hier findest du 20 (neue) Brainteaser, um deine Denkmuskeln zu trainieren. Klick auf "Tipp anzeigen", um einen Hinweis darauf zu bekommen, ob du auf der richtigen Spur bist.

1. Das Alien beim Sonnenbaden

Mister Mxyzptlk wiegt 1.500 kg und besteht zu 99% aus Schleim (der Rest ist Diamant).

Beim Sonnenbaden verliert es an Flüssigkeit, sodass es nur noch zu 97% aus Schleim besteht.

Wie viel wiegt Mister Mxyzptlk jetzt?

Tipp anzeigenLösung zeigen

Tipp: Bestimmte das Diamant-Gewicht und rechne von diesem ausgehend.

Lösung:

1. Vor dem Sonnenbaden entsprach der Nicht-Schleim-Anteil 1% und damit 15 kg.

2. Nach dem Sonnenbaden beträgt der Nicht-Schleim-Anteil 3%, liegt aber immer noch bei 15 kg. Rechnerisch wiegt Mister Mxyzptlk damit nur noch 500 kg, also ein Drittel.

3. Immer schön eincremen.

2. Iron Man

Du nimmst am Iron Man teil. 852 Meter vor der Ziellinie überholst du den Viertplatzierten. Welchen Platz hast du jetzt?

Tipp anzeigenLösung zeigen

Tipp: Das ist keine Trickfrage.

Lösung: Den vierten.

3. Werwolf Weihnachtsmann & der Dieb

Werwolf Weihnachtsmann lässt 9 Wichtel je 9 Klingelglöckchen à 9 g Gold herstellen.

Einer der Wichtel betrügt, indem er pro Klingelglöckchen 1g Gold unterschlägt!

Wie kann Werwolf Weihnachtsmann mit einer grammgenauen Küchenwaage und nur einmaligem Wiegen herausfinden, wer betrogen hat?

Tipp anzeigenLösung zeigen

Tipp: Werwolf W. muss aus dem Ergebnis ablesen können, wer betrogen hat. Deshalb darf er nicht von jedem Wichtel gleich viele Glöckchen wiegen.

Lösung:

1. Werwolf Weihnachtsmann nummeriert seine Wichtel durch und wiegt dann pro Wichtel die Anzahl an Klingelglöckchen, die dessen Nummer entspricht. Also 1+2+3+4+5+6+7+8+9 = 45 Klingelglöckchen.

2. Der Wert, um den das Ergebnis von 405 g abweicht (= so viel hätten die Glöckchen gemeinsam gewogen, wenn jedes 9 g schwer gewesen wäre), entspricht der Nummer des Diebs.

Brainteaser 4 bis 12

4. Die Mondsteine

Du hast 9 Mondsteine und eine Apothekerwaage mit zwei Waagschalen. Alle Mondsteine wiegen gleich viel, nur einer ist minimal schwerer als die anderen. Wie kannst du mit nur zweimaligem Wiegen den schwereren Mondstein ausfindig machen?

Tipp anzeigenLösung zeigen

Tipp: Du musst zunächst 3 gegen 3 Steine wiegen.

Lösung:



1. Du wiegst zunächst 3 Steine auf einer, 3 auf der anderen Seite.
- Ist die Waage ausgeglichen, befindet sich der gesuchte Stein nicht auf der Waage.
- Ist die Waage nicht ausgeglichen, muss der schwerere Stein sich auf der tieferliegenden Seite befinden.
- In beiden Fällen erhältst du eine Menge von 3 Steine, unter denen der gesuchte sein muss.



2. Du wiegst 2 der 3 Steine, die den schwereren enthalten. Es gilt erneut:
- Ist die Waage ausgeglichen, ist der gesuchte Stein nicht auf der Waage.
- Ist die Waage nicht ausgeglichen, muss der schwerere Stein sich auf der tieferliegenden Seite befinden.

3. In allen Fällen bleibt der gesuchte Stein eindeutig zurück.

5. Karlheinze & die Currysuppe

Karlheinze soll aus einem Fass Currysuppe genau 4 Deziliter servieren. Sie hat aber nur eine 5-Deziliter-Kelle und eine 3-Deziliter-Kelle.

Wie schafft sie das?

Tipp anzeigenLösung zeigen

Tipp: Karlheinze muss den Inhalt der großen Kelle während des Abmess-Vorgangs einmal ins Fass zurückschütten.

Lösung:

1. Sie kippt den Inhalt der kleineren Kelle zweimal in die große, bis diese voll ist. Übrig bleibt 1 Deziliter in der kleinen Kelle.

2. Dann schüttet sie den Inhalt der großen Kelle zurück ins Fass und den verbliebenen Deziliter aus der kleinen in die große Kelle.

3. Mit der kleinen Kelle ergänzt sie nochmals 3 Deziliter zu dem Deziliter in der großen Kelle.

4. Guten Appetit.

6. Schlitzohr Derrick

Derrick und Schimanski beginnen bei der Zahl 2. Sie sollen abwechselnd eine Zahl zwischen 1 und 10 addieren, sodass die Summe immer größer wird.

Wer schließlich mit seiner letzten Addition genau bei 100 landet, gewinnt ein goldenes Polizeiauto.

Derrick eröffnet mit: 2 + 10 = 12.

Warum kann Schimanski nicht mehr gewinnen?

Tipp anzeigenLösung zeigen

Tipp: Um sicher die 100 zu treffen (und zu gewinnen), braucht Derrick eine Strategie, mit der er zuvor sicher die 89 trifft. Wie kann er jede mögliche Zahl, die Schimanski nennt, so parieren, dass diese Bedingung eintritt?

Lösung: Egal, welche Zahl Schimanski nennt, Derrick wird immer eine Zahl ergänzen, die mit Schimanskis Zahl zusammen 11 ergibt. Nimmt Schimanski eine 1, nimmt Derrick eine 10 usw.

So schafft es Derrick, nach seiner 8. Ansage immer auf 89 zu stehen. Egal, was Schimanski jetzt sagt, Derrick wird mit seinem 9. Zug die 100 treffen und gewinnen.

7. Die Wunderkerzen des Papstes

Papst Pampelmus hat zwei Wunderkerzen, die jeweils genau zwei Stunden brennen. Die Geschwindigkeit, mit der sie abbrennen, ist jedoch unregelmäßig. Wie kann Papst Pampelmus mit diesen Wunderkerzen genau 1,5 Stunden abmessen?

Tipp anzeigenLösung zeigen

Tipp: Wunderkerzen kann man nicht nur an einer Seite anzünden.

Lösung: 1. Er zündet eine Wunderkerze an beiden Enden, die andere an nur einem Ende an. Wenn die doppelt brennende Kerze erloschen ist, ist eine Stunde vergangen.

2. Dann zündet Papst Pampelmus die halb abgebrannte Kerze an beiden Enden an. Wenn sie erlischt, sind noch mal 30 Minuten vergangen.

8. Die Eier der Tyrannosaurier

1,5 Tyrannosaurier Rex legen an 1,5 Tagen 1,5 Eier. Wie viele Eier legt ein Tyrannosaurus Rex an drei Tagen?

Tipp anzeigenLösung zeigen

Tipp: Es sind nicht drei Eier. Nutz einen Dreisatz, um die Lösung zu finden.

Lösung: Zwei.

9. Der Haken? Der Anker!

Du bist in einem Boot auf einem See. Du holst den Anker ein. a) Sinkt oder b) steigt der Wasserspiegel? c) Oder bleibt er gleich?

Tipp anzeigenLösung zeigen

Tipp: Du benötigst eine ungefähre Vorstellung davon, wie Auftrieb funktioniert.

Lösung: Er steigt.

Die Dichte des Ankers ist höher als die von Wasser. Wenn er also auf das Boot drückt, verdrängt er damit so viel Wasser, wie seiner Masse entspricht (sagen wir: 20 l, weil der Anker 20 kg wiegt). Auf dem Grund des Sees liegend, verdrängt der Anker aber auf jeden Fall weniger Wasser, weil die verdrängte Wassermenge dort nur noch seinem Volumen entspricht.

10. Kriemhild auf der Rolltreppe

Kriemhild will wissen, wie viele Stufen die Rolltreppe im Kaufhaus des Westens hat. Die Rolltreppe rollt von oben nach unten in gleichbleibender Geschwindigkeit.

Geht sie die Treppe hoch (entgegen der Fahrtrichtung), zählt sie 120 Stufen unter sich. Geht sie die Treppe hinunter, sind es nur 80.

Wie viele Stufen wären zu sehen, wenn die Treppe stillstehen würde? (100 ist übrigens falsch.)

Tipp anzeigenLösung zeigen

Tipp: Diese Aufgabe kann mit einem Gleichungssystem gelöst werden, das die Anzahl der Stufen gleichsetzt, die zu sehen sind, wenn die Treppe stillsteht.

Lösung: 96 Stufen.

1. In der Zeit, die Kriemhild nach oben bzw. unten braucht, verschwindet eine Anzahl von Stufen unter der Treppe bzw. taucht gleichzeitig wieder oben auf.

2. Diese Anzahl verschwundener/auftauchender Stufen muss im gleichen Verhältnis zueinander stehen wie die Zeit, die Kriemhild jeweils auf der Treppe verbringt, die wieder im gleichen Verhältnis steht wie die Zahl der Stufen, die sie jeweils zählt (also 120 zu 80).

3. Die Lösung liefert nun ein Gleichungssystem:

Im Stillstand sichtbare Stufen = 120 – 120x (für den Lauf gegen die Rollrichtung)
Im Stillstand sichtbare Stufen = 80 + 80x (für den Lauf mit der Rollrichtung)
Führt zu: 80 + 80x = 120 – 120x
Führt zu: x = 1/5
Führt zu: x in eine der ersten zwei Gleichungen einsetzen.
Führt zu: Im Stillstand sichtbare Stufen = 96

11. Canale Deckele

Warum sind Kanaldeckel eigentlich rund? Skizziere verschiedene Lösungen.

Tipp anzeigenLösungen zeigen

Tipp: Welche Nachteile hätten quadratische Kanaldeckel?

Lösungen: Mögliche Antworten könnten sein:

1. Weil sie an die runden Schächte angepasst wurden, die darunterlagen. Die Schächte sind deshalb rund, weil man beim Bohren runde Durchmesser erhält.

2. Wären sie viereckig, könnten sie in den Schacht fallen, da die Diagonale des Schachts länger ist als eine Kante des Deckels.

3. Damit man sie rollen kann.

12. Pizza Montessori

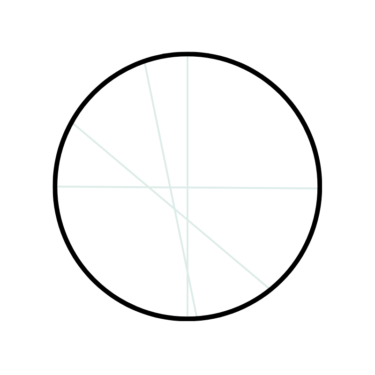
Primbold soll eine kreisrunde Pizza Montessori mit vier geraden, senkrechten Schnitten so zerschneiden, dass möglichst viele Stücke entstehen.

Die Stücke müssen am Ende nicht gleich groß sein, dürfen aber beim Schneiden weder über-, hinter- oder nebeneinandergelegt werden.

Wie viele Stücke erhält Primbold maximal?

Tipp anzeigenLösung zeigen

Tipp: Jeder Schnitt sollte möglichst viele neue Stücke produzieren.

Lösung: Elf.

Und zwar dann, wenn jeder Schnitt alle bisherigen Schnitte kreuzt.

Brainteaser 13 bis 20

13. Manhattan

Wie viel wiegt Manhattan? Produziere eine Lösungsskizze.

Tipp anzeigenLösungsskizze zeigen

Tipp: Versuche, möglichst plausible Annahmenn zu treffen. Du musst wissen, wie Volumen berechnet wird, und wie Volumen-Maßstäbe umgerechnet werden.

Lösungsskizze: Wenn du schon mal in Manhattan warst, wirst du wissen, dass es von 12 Avenues durchschnitten wird, zwischen denen Häuserblocks liegen. Nimm für jeden Häuserblock 200 m Breite an, kommst du auf eine Breite von 2,4 km (de facto sind es zwischen 1,3 und 3,7 km). Da Manhattan deutlich länger als breit ist, nimm den 8-fachen Wert der Breite an: 19,2 km (de facto 21,6 km). Daraus ergäbe sich eine Grundfläche von 46 km² (de facto sind es 59,5 km² Landfläche). Nun zur "Tiefe", die sich natürlich nicht genau bestimmen lässt. Nimmst du 10 km an, ergeben sich 460 km³. Gehst du davon aus, dass ein Kubikmeter Granit 1 t wiegt (de facto sind es 2,6 t), dann kannst du 1 Milliarde t pro km³ annehmen und damit 460 Milliarden t für Manhattan. Für Bebauung, Menschen und Verkehrsmittel sollst du weitere Gewichtsannahmen treffen.

14. Tiere auf der Arche

Wie viele Tiere nahm Moses mit auf die Arche? Skizziere eine Lösung.

Tipp anzeigenLösung zeigen

Tipp: Lies die Frage noch mal genau.

Lösung: Keins. Es war nicht Moses, der die Arche baute, sondern Noah.

15. Smarties im Smart

Wie viele Smarties passen in einen Smart? Produziere eine Lösungsskizze.

Tipp anzeigenLösungsskizze zeigen

Tipp: Du musst wissen, wie Volumen und Kreisformen berechnet werden. Du musst Volumen-Maßstäbe umrechnen können.

Lösungsskizze:

1. Ein Smartie hat etwa einen Durchmesser von 1 cm und ist 0,5 cm hoch. Da ein Smartie rund ist, hat es etwa eine Oberfläche von 0,8 cm². Mit der geschätzten Höhe ergibt sich ein Volumen von 0,4 cm³ pro Smartie.

2. Stell dir dann einen Smart vor. Er ist etwa so breit wie andere Kleinwagen, also etwa 1,5 m, dazu sehr kurz; nimm als Länge 2,5 m an. Die Dachhöhe dürfte einem Durchschnitts-Erwachsenen bis zur Schulter reichen, nimm also 2,5 x 1,5 x 1,5 m als Grundmaße an, was 5,6 m³ Volumen ergibt. Zieh etwas für Motor, Innenausstattung und Karosseriehöhe ab, dann verbleiben ca. 4 m³, was 4 Millionen cm³ entspricht.

3. Damit passen rechnerisch 10 Millionen Smarties in einen Smart. Wenn du noch davon ausgehst, dass zwischen den einzelnen Smarties etwas Luft bleiben wird, musst du die Zahl etwas nach unten korrigieren.

16. Tankstellen in Deutschland

Wie viele Tankstellen existieren in Deutschland? Produziere eine Lösungsskizze.

Tipp anzeigenLösungsskizze zeigen

Tipp: Am einfachsten gehst du von eigenen Erfahrungswerten aus und skalierst diese hoch.

Lösungsskizze:

1. Wie viele Menschen wohnen in deinem Heimatort? Wie viele Tankstellen gibt es dort? Auf wieviele Menschen kommt also etwa eine Tankstelle?

2. Rechne deinen "Tankstellenquotienten" mit einem Dreisatz auf die Gesamtbevölkerung hoch. Addiere unter Umständen eine dreistellige Zahl von Tankstellen, die sich an deutschen Autobahnen befinden. Auf welche Zahl kommst du? Die korrekte Anzahl beträgt rund 15.000.

Auf ähnliche Weise lassen sich folgenden Fragen näherungsweise beantworten: Wie viel Zahnpasta wird in Deutschland pro Jahr verbraucht? Wie viele Hunde gibt es in den USA? Wie viele Hotels gibt es in Bayern?

17. Vier Töchter

Marys Mutter hat vier Töchter. Drei heißen April, May und June. Wie heißt die vierte Tochter?

Tipp anzeigenLösung zeigen

Tipp: Lies die Frage noch mal genau.

Lösung: Mary.

18. Deutsche Katzen

Wie viele Katzen leben in deutschen Haushalten? Gib an, wie du auf die Anzahl kommst.

Tipp anzeigenLösungsskizze zeigen

Tipp: Am einfachsten gehst du von eigenen Erfahrungswerten aus und skalierst diese hoch.

Lösungsskizze: Wie viele Menschen in deinem Bekanntenkreis haben Katzen? Und wie viele Katzen leben jeweils in einem Haushalt? Ist dein Bekanntenkreis repräsentativ? Nehmen wir an, eine Katze käme schätzungsweise auf 10 Personen. In Deutschland leben 82,1 Millionen Menschen – also kannst du 8 Millionen Katzen als plausible Schätzung angeben.

De facto sind es übrigens 12,9 Millionen (2015).

19. Licht im Kühlschrank

Wie kannst du herausfinden, ob das Licht im Kühlschrank brennt, wenn die Tür zu ist?

Tipp anzeigenLösungen zeigen

Tipp: Es gibt keine Musterlösung. Zeige verschiedene Möglichkeiten auf.

Lösungen: Mögliche Lösungen:
- Gleichmäßig Moos im Kühlschrank säen, nach einiger Zeit überprüfen, ob es sich um die Lichtquelle herum angesammlt hat. Falls ja, brennt das Licht im Kühlschrank.
- Überprüfen, ob der Strombedarf des Kühlschranks sich bei geöffneter und geschlossener Tür unterscheidet.
- Lampe einsetzen, die Wärme abstrahlt. Direkt nach dem Öffnen der Türe überprüfen, ob die Lampe bereits heiß ist (oder gerade erst beginnt, heiß zu werden). - Fotopapier in den Kühlschrank legen, abwarten, ob es belichtet wird (Problem allerdings: Das Fotopapier darf zuvor nicht schon belichtet werden).

20. Im Aldi Geld machen

Wie viel Geld liegt in einer Aldi-Filiale pro Tag auf dem Boden?

Tipp anzeigenLösungsskizze zeigen

Tipp: Es gibt keine Musterlösung. Zeig einen rechnerischen Weg auf, den Betrag möglichst plausibel einzuschätzen.

Lösungsskizze: Eine Aldi-Filiale hat pro Tag etwa 12 Stunden geöffnet. Pro Stunde dürften sich etwa 100 Einkäufer dort einfinden, was 1.200 pro Tag entspricht. Etwa jeder 50. Besucher könnte eine Münze verlieren, im Schnitt vielleicht 50 Cent. Jeder 500. Besucher vielleicht einen Schein, im Schnitt im Wert von 10,- Euro. Also liegen in einer Aldi-Filiale im Schnitt 32 Euro pro Tag auf dem Boden.